Podstawy teoretyczne
Układy koloidowe pozostają stabilne, gdy dyfuzja (ruchy Browna) cząsteczek dominują nad grawitacją oraz gdy cząsteczki nie agregują. Pierwszy z tych warunków łatwo spełnić dobierając odpowiednio drobne cząsteczki (liczba Pécleta) lub zrównując gęstości cząsteczek i rozpuszczalnika. Drugi warunek wymaga ustalenia oddziaływań pomiędzy cząsteczkami zapobiegających agregacji. Najczęściej tę rolę pełnią oddziaływania elektrostatyczne, co oznacza, że cząsteczki w zawiesinie obdarzone są łądunkiem elektrycznym.
Układy koloidowe stabilizowane ładunkiem charakteryzują się złożonymi właściwościami strukturalnymi i ciekawą dynamiką. Punktem odniesienia dla nich są układy koloidów neutralnych elektrycznie, w których jedynym parametrem wyznaczającym zachowanie zawiesiny jest ułamek objętościowy \(\phi\). W koloidach takich dopiero istotny wzrost wartości \(\phi\), oznaczający stłoczenie cząsteczek koloidowych, wywołuje efekty widoczne zarówno we właściwościach strukturalnych w postaci pojawienia się uporządkowania przestrzennego cząsteczek jak i w ich dynamice w postaci spowolnienia dyfuzji własnej i skomplikowanej postaci zależności współczynnika dyfuzji kolektywnej od wielkości wektora rozpraszania \(q\) (Russel et al. 1989).

Rys. 1. Rodzaje jonów występujące w zawiesinie koloidowej.
W przypadku obdarzenia cząsteczek koloidu ładunkiem wspomniane zjawiska mogą się pojawiać już dla bardzo niewielkich wartości \(\phi\), a dodatkowymi parametrami układu stają się ładunek cząsteczki \(Z\) oraz stężenie dodanej soli \(C_s\) i stała dielektryczna \(\epsilon\) rozpuszczalnika.
W najprostszym przybliżeniu (liniowej wersji rozwinięcia wirialnego) różne parametry charakteryzujące cząsteczki koloidowe zmieniają się liniowo z ułamkiem objętościowym \(\phi\). Dotyczy to np. odwrotności pozornej masy cząsteczkowej, ściśliwości osmotycznej, współczynnika dyfuzji. NAchylenie tej zależności, wyrażone poprzez pierwszy współczynnik wirialny jest miarą siły oddziaływań międzycząsteczkowych. Oddziaływania te prowadzą do lokalnego uporządkowania cząsteczek.
Miarą tego uporządkowania jest funkcja korelacji dwójkowych \(g(r)\) zdefiniowana jako prawdopodobieństwo znalezienia cząsteczki w odległości \(r\) od innej cząsteczki zawiesiny (Nägele 1996).
\[g(r)=\frac{1}{n^2}\langle \sum_{i,j=1}^{N} \frac{1}{V} \delta \left( r-R_i + R_j \right) \rangle ,
\]
gdzie \(n\) jest stężeniem liczbowym cząsteczek koloidowych, a \(V\) jest objętością próbki. Wielkość \(4\pi n g(r) r^2 dr\) to średnia liczba cząsteczek w sferycznej otoczce o promieniu \(r\) i grubości \(dr\) wybranej cząsteczki. Miarą rosnącego porządku w zawiesinie są rosnące oscylacje funkcji \(g(r)\) z wyraźnym maksimum dla \(r\) bliskiego średniej odległości międzycząsteczkowej \(\langle r \rangle = n^{-1/3}\). Ponieważ funkcja \(g(r)\) jest bardzo trudno osiągalna doświadczalnie, zazwyczaj obliczany jest na jej podstawie tzw. czynnik struktury \(S(q)\), czyli funkcja będąca formalnie transformatą Fouriera funkcji \([g(r)-1]\), a jednocześnie w naturalny sposób modulująca natężenie promieniowania rozpraszanego przez zawiesinę we wszystkich eksperymentach rozproszeniowych.
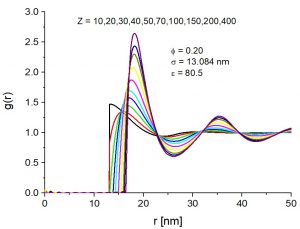
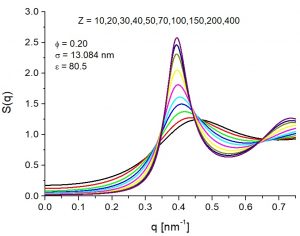
Rys. 2. Funkcje korelacji radialnych \(g(r)\) oraz czynniki struktury \(S(q)\) obliczone przy pomocy modelu RMSA dla zawiesiny naładowanych kulek o średnicy \(\sigma = 13.084\) nm w 10 mM wodnym roztworze jednowartościowej soli. Wysokość pików rośnie z wartością ładunku \(Z\) makrojonów.
Oddziaływania elektryczne pomiędzy wszystkimi składnikami zawiesiny przedstawionej schematycznie na Rys. 1 są dość złożone i przypominają te zachodzące w plazmie. Schemat postępowania polega na uproszczeniu zagadnienia do obliczenia potencjału elektrycznego wokół makrojonu otoczonego chmurą mikrojonów, a następnie energii oddziaływań makrojonów otoczonych takim potencjałem. Koncepcja ta nosi nazwę jednoskładnikowej makro-cieczy (ang. one component macro-fluid) i stosowana jest szeroko w fizykochemii koloidów (Nägele 1996).
Punktem wyjścia w teoretycznym opisie układów naładowanych cząsteczek w roztworze jest koncepcja jednoskładnikowej makro-cieczy, która swoimi parametrami uwzględnia obecność i wpływ mikrojonów na zachowanie cząsteczek koloidu. W przybliżeniu oddziaływań dwójkowych zachowanie to zdeterminowane jest przez sumę energii oddziaływań wszystkich par makrojonów w roztworze. Energię oddziaływania pary cząsteczek uzyskamy po obliczeniu potencjału, jakim otoczony jest makrojon zanurzony w rozpuszczalniku zawierającym określoną liczbę mikrojonów: przeciwjonów, które oddysocjowały z cząsteczek koloidu oraz zdysocjowanych jonów dodanej soli. Potencjał \(\phi(r)\) wokół pojedynczego makrojonu znajduje się rozwiązując równanie Poisona-Boltzmanna:
\[\Delta \phi (r)=-\frac{1}{\epsilon \epsilon_s} \sum_i z_i n_{i0} e^{-\frac{z_i \phi (r)}{k_B T}} \]
gdzie \(z_i\) i \(n_i\) to odpowiednio ładunki i stężenia mikrojonów poszczególnych rodzajów, \(\epsilon_s\) to względna stała dielektryczna rozpuszczalnika, a \(\epsilon_0\) to stała dielektryczna próżni.
Rozwiązanie zlinearyzowanej postaci tego równania podali Debye i Hückel (1923)
\[\phi_{DH}(r)=\frac{Z}{e}\lambda_B k_B T \frac{e^{-\kappa r}}{r}.\]
We wzorze (5) pojawiły się dwie charakterystyczne długości charakteryzujące właściwości makro-cieczy: długość Bierruma \(\lambda_B\), wyrażająca odległość na jakiej energia oddziaływania elektrostatycznego dwóch ładunków elementarnych \(e\) równa jest \(k_B T\) oraz długość ekranowania Debye’a \(\lambda_D = 1/\kappa\) określająca charakterystyczną odległość wykładniczego zaniku oddziaływań w stosunku do zależności Coulomba.
\[\lambda_B = \frac{e^2}{4\pi \epsilon_s \epsilon_0 k_B T}\quad \lambda_D = \frac{1}{\kappa}=\sqrt{\frac{\epsilon_s \epsilon_0 k_B T}{e^2\sum_a z_a^2 n_{a0}}}=\left( 4 \pi \lambda_B \sum_a z_a^2 n_{a0}\right)^{-\frac{1}{2}}\]
Na bazie potencjału Debye’a-Hückel’a udało się obliczyć energię oddziaływania \(u(r)\) pary makrojonów:
\[\frac{u_{DLVO}(r)}{k_B T}=Z^2\lambda_B \left( \frac{e^{\kappa a}}{1+\kappa a}\right)^2 \frac{e^{-\kappa r}}{r}.\]
We wzorze (8) \(a\) jest promieniem cząsteczki koloidu, a litery DLVO pochodzą od dwu par naukowców, którzy jako pierwsi podali postać \(u(r)\): Derjaguin i Landau (1941) oraz Verwey i Overbeek (1948).
Równania (7-8) są punktem wyjścia wszystkich modeli bazujących na koncepcji cieczy jednoskładnikowej.
Strukturę cząsteczek w zawiesinie ilościowo wyraża funkcja korelacji radialnych \(g(r)\) zdefiniowana we wstępie (Równ. 1). Czynnik struktury \(S(q)\) jest transformatą Fouriera funkcji \([g(r) – 1]\) (Nägele 1996)
\[S(q)=1+n \int d^3r e^{iqr}\left[ g(r)-1 \right]. \]
Czynnik struktury \(S(q)\) może być wyznaczony doświadczalnie w eksperymencie rozproszeniowym.
Wyznaczenie \(g(r)\) lub \(S(q)\) przy znajomości energii oddziaływania pomiędzy parami jonów wymaga zastosowania równania Ornsteina-Zernicke, metody zapożyczonej z teorii cieczy prostych:
\[h(r)=c(r)+n \int d^3 r’ c\left(|r-r’| \right) h(r’)\]
gdzie tzw. całkowita funkcja korelacji \(h(r) = g(r) – 1 \) wyrażona jest w postaci sumy tzw. funkcji korelacji bezpośrednich \(c(r)\) oraz wyrażenia całkowego zawierającego korelacje pośrednie, a więc wpływ jednej cząsteczki na drugą za pośrednictwem trzeciej. Do rozwiązania równania Ornsteina-Zernicke potrzebne są tzw. relacje domknięcia.
MSA (Mean spherical approximation)
Jedna z najprostszych relacji domknięcia, w której postuluje się \(c(r) = -u(r)/k_B T\). Zaletą jest analityczna postać rozwiązania na \(g(r)\):
\[g^{MSA}(r)=1-\frac{u(r)}{k_B T}, \quad r>\sigma\]
RMSA (Rescaled mean spherical approximation)
Pomysł (Hansen & Hayter 1982) polegał na wprowadzeniu do obliczeń MSA fikcyjnej średnicy cząsteczek \(\sigma’\) (odpowiednio przeskalowanej) przy postawieniu warunku \(g(\sigma’)=0\).
Cechy RMSA:
• Brak rozwiązań analitycznych,
• Stosunkowo prosty i szybki kod obliczeniowy,
• Niedoszacowanie porządku, tzn. taka sama wysokość piku \(S(q)\) wymaga wprowadzenia ładunków wyższych niż w innych modelach.
Percus-Yevick (PY)
Daje rozwiązanie analityczne dla oddziaływań typu „twarde kule” (Percus & Yevick 1958).
\[c(r)=g(r) \left[ 1- \exp \left( \frac{u(r)}{k_B T} \right) \right] \]
Model ten jest bardzo popularny ze względu na szereg zastosowań oraz jako punkt odniesienia dla układów oddziałujących.
HNC – hypernetted chain approximation (van Leeuwen et al.1959)
\[g(r)=\exp \left( \frac{u(r)}{k_B T}+h(r)-c(r) \right)\]
HNC działa słabo dla twardych kulek, natomiast znacznie lepiej dla miękkich oddziaływań, m.in. elektrostatycznych.
Rogers-Young (RY)
Łączy ona cechy dwu innych metod: Percusa-Yevicka oraz HNC w proporcjach regulowanych przez funkcję mieszania \(f(r) = 1 – e^{-\alpha r}\) z parametrem mieszania \(\alpha \ (0 < \alpha < \infty)\) (Rogers and Young 1984).
\[g(r)=e^{-\frac{u(r)}{k_B T}}\lbrace 1+\frac{1}{f(r)}\left[ e^{f(r)\left[ h(r)-c(r) \right] } -1 \right] \rbrace. \]
Zaletą jest dobra zgodność z symulacjami komputerowymi, ale wadą stosunkowo długi czas obliczeń związany z koniecznością znalezienia optymalnego parametru mieszania \(\alpha\).
Dzięki uprzejmości prof. Gerharda Naegele z Forschungszentrum Juelich, w Zakładzie dysponujemy sprawdzonymi programami do obliczeń \( S(q)\) i \(g(r)\) z użyciem schematu RMSA oraz Rogersa-Younga. Napisany przez nas interfejs graficzny czyni z niego doskonałe narzędzie do symulacji parametrów zawiesin koloidowych cząsteczek obdarzonych ładunkiem. Wyniki obliczeń z użyciem tego narzędzia można znaleźć we wszystkich naszych pracach z Gerhadem Naegele jako współautorem.
Ostatnio najciekawsze z tej dziedziny wydają się nasze prace dotyczące badania lokalnej struktury koloidów, ze szczególnym uwzględnieniem warunków, w jakich krystalizują. W badania te włączył się ostatnio dr Sebastian Wołoszczuk z naszego Wydziału, dokonując symulacji Monte Carlo takich układów.
Wyniki badań wpływu oddziaływań na dyfuzję i strukturę roztworu w różnych układach
Rozwinięcie wirialne zostało zastosowane w pracach dotyczących micel wzorcowych i nowych surfaktantów, powstałych we współpracy z grupą prof. Wilk z Politechniki Wrocławskiej (Bieniecki et al. 1997a, Bieniecki et al. 1997b).
Nieco egzotyczny model sprzężonych modów (w którym dyfuzja mikrojonów moduluje dyfuzję makrojonów) uwzględniliśmy w pracach dotyczących pomiarów dyfuzji oligomerów DNA oraz ferrytyny (Liu et al. 1998, Skibinska et al. 1999, Włodarczyk et al. 1999, Liu et al. 2000, Haeussler et al. 2002, Gapinski et al. 2005).
Obliczenia oparte na modelu OCM z równaniami Ornsteina-Zernicke zastosowano do analizy wyników PCS, SAXS i XPCS zawiesin koloidowych cząsteczek polimerowych i krzemionkowych: Banchio et al. 2006, Gapinski et al. 2007, Patkowski et al. 2008, Gapinski et al. 2009, Gapinski et al. 2010, Gapinski et al. 2012, Gapinski et al. 2014.
Największym wyzwaniem są ukłądy, w których jednocześnie zmieniają się rozmiary lub kształt cząsteczek oraz ich oddziaływania. Przykładem takich obiektów są micele (Gapinski et al. 2010) oraz białka nieuporządkowane, którymi zainteresowaliśmy się dzięki współpracy z Katedrą Biochemii Wydziału Chemicznego Politechniki Wrocławskiej (Poznar et al. 2017).