Dlaczego warto?
Szkło jest materiałem o mikroskopowej strukturze cieczy i makroskopowych mechanicznych własnościach ciała stałego. Najczęściej szkło otrzymuje się przez gwałtowne chłodzenie ciecz do temperatur poniżej temperatury topnienia \(T_m\) w sposób pozwalający uniknąć krystalizacji. Temperatura przejścia szklistego \(T_g\approx2T_m/3\) maleje ze spadkiem prędkości chłodzenia. Przejście szkliste nie jest przejściem fazowym 1-go ani 2-go rodzaju. Lepkość i czas relaksacji strukturalnej rosną o ok. 14 rzędów wielkości przy schładzaniu cieczy od \(T_m\) do \(T_g\) i zależność tą można przedstawić w postaci tzw. wykresu Angella [1] Rys.1.
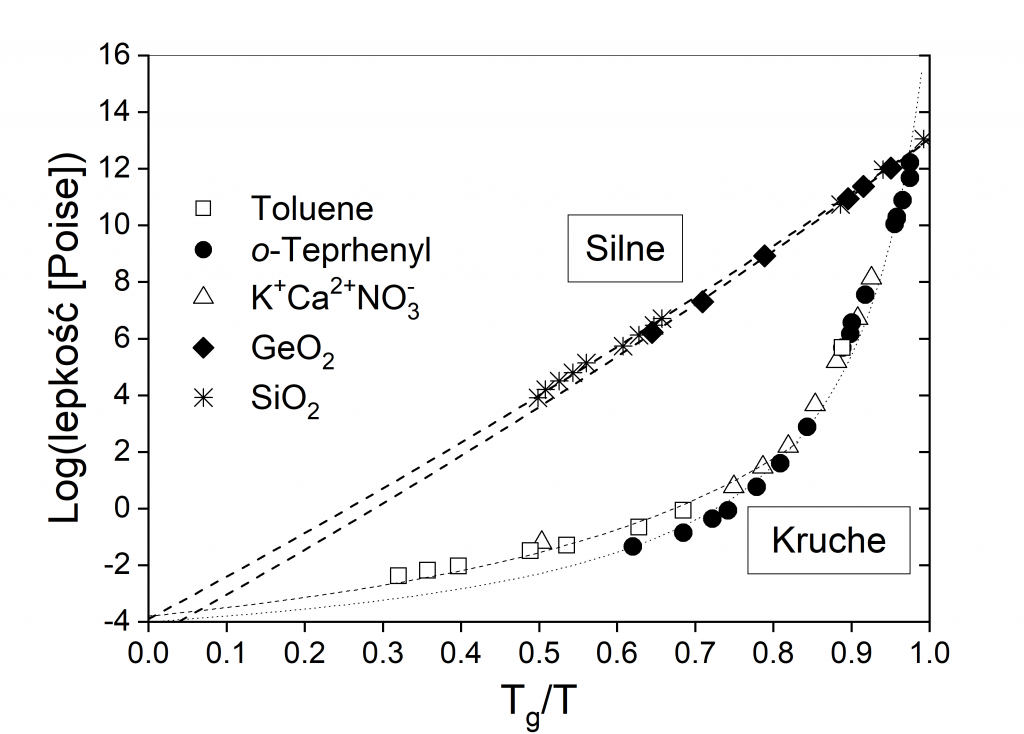Rys.1 Lepkość cieczy przechłodzonej w zależności od \(T_g/T\). Nachylenie krzywej w punkcie \(T_g/T =1\) określa kruchość cieczy [1].
Zależność lepkości \(\eta\) (czasu relaksacji \(\tau_\alpha\)) od temperatury wyrażana jest przy pomocy równania Vogela – Fulchera – Tammanna (VFT) [2]:
\[\eta=\eta_0 exp(\frac{D T_0}{T-T_0})\] \[\tau=\tau_0 exp(\frac{D T_0}{T-T_0})\]
gdzie \(\eta_0\), \(\tau_0\), i \(T_0\) są stałymi materiałowymi, \(D\) jest inną miarą kruchości. \(T_0\) jest temperaturą o kilkadziesiąt stopni niższą od \(T_g\) i jest w przybliżeniu równa temperaturze Kautzmanna \(T_K\), poniżej której ekstrapolowana wartość entropii cieczy jest niższa niż entropia kryształu.
Proces relaksacji strukturalnej (relaksacja \(\alpha\)) w cieczach przechłodzonych opisywany jest funkcją korelacji typu Kohlrauscha – Williamsa – Wattsa (KWW) [3]:
\[g(t)=exp\left[-\left(
\frac{t}{\tau_{KWW}}
\right)^{\beta_{KWW}}
\right], 0<\beta_{KWW}\le1
\]
Średni czas relaksacji \(\left<\tau_{KWW}\right>\) zdefiniowany jest jako:
\[\left<\tau_{KWW}\right>=\frac{\tau_{KWW}}{\beta_{KWW}}\Gamma\left(\frac{1}{\beta_{KWW}}\right)\]Gdzie \(\Gamma\left(\frac{1}{\beta}\right)\) jest funkcją Gamma. Zazwyczaj parametr \(\beta_{KWW}\) zmienia się od ok. 1 w wysokiej temperaturze do ok. 0,5 w \(T_g\) , co odpowiada rozkładowi czasów relaksacji obejmującemu kilka rzędów wielkości [4].
Zatem ciecze przechłodzone charakteryzują się trzema niezwykłymi własnościami:
- Silnym wzrostem czasu relaksacji strukturalnej i lepkości o 13-15 rzędów wielkości w wąskim zakresie temperatur pomiędzy \(T_m\) and \(T_g\),
- Szerokim rozkładem czasów relaksacji obejmującym wiele rzędów wielkości i opisywanym funkcją korelacji typu KWW
- Różnym charakterem zależności czasów relaksacji i lepkości od temperatury, zależnym od materiału i określonym jako jego kruchość.
Zrozumienie natury fizycznej tych trzech własności i ich związku z budową chemiczną cieczy przechłodzonych jest jednym z ważnych, nierozwiązanych problemów dzisiejszej fizyki amorficznej fazy skondensowanej. Mimo bardzo szerokiej bazy danych doświadczalnych dla różnorodnych cieczy przechłodzonych [5] nie udało się stworzyć teorii mikroskopowej wyjaśniającej wszystkie niezwykłe dynamiczne i strukturalne własności tych materiałów.
- C. A. Angell, w Relaxations in Complex Sysyrems, wyd. K. Ngai, G. B. Wright (National Technical Information Service, U.S. Department of Commerce, Springfield, VA, (1985).
- T. Kanaya, A. Patkowski, E. W. Fischer, J. Seils, H. Gläser and K. Kaji, Light Scattering Studies on Long-Range Density Fluctuations in a Glass Forming Polymer, Acta Polymerica, 45, 137 (1994).
- G. Williams, D. C. Watts, Trans. Farraday Soc. 66, 80 (1970).
- C. P. Lindsey, G. D. Patterson, J. Chem. Phys. 73, 3348 (1980).
- K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer (2011).
Klastery – historia i teraźniejszość
Na początku lat 90-tych zaproponowano interpretację niektórych wyników eksperymentalnych opartą na istnieniu dynamicznych struktur w przechłodzonych molekularnych cieczach [1] i polimerach [2].
- Fischer, E W; Meier, G; Rabenau, T; Patkowski, Adam; Steffen, W; Thoennes, W Density fluctuations around the glass-transition of low molecular weight glass-forming liquids Journal of Non-Crystalline Solids, 131-133 , pp. 134–138, 1991
- Kanaya, T; Patkowski, Adam; Fischer, E W; Seils, J; Glaeser, H; Kaji, K Light scattering studies on long-range density fluctuations in a glass-forming polymer Acta Polymerica, 45 (3), pp. 137–142, 1994
Temperatura czy objętość swobodna – skalowanie dynamiki cieczy przechłodzonych
Chociaż w sekcji Dlaczego warto? omówiono tylko zachowanie cieczy przechłodzonych poprzez obniżenie temperatury, to w rzeczywistości równie skutecznie przechłodzenia cieczy oraz przeprowadzenia jej w stan szklisty można dokonać poprzez zwiększanie ciśnienia hydrostatycznego w próbce. Przez dłuższy czas brakowało spójnego opisu uwzględniającego oba te efekty. Dane prezentowane były albo w postaci izobar jako zależności wyłącznie temperaturowe opisywane funkcjami typu VFT, albo w postaci izoterm jako zależności czysto ciśnieniowe (gęstościowe) opisywane ciśnieniowymi analogami funkcji VFT. W tych ostatnich eksponowano m.in. pojęcie objętości swobodnej (free volume), której wartość w ogromnej mierze miała wyznaczać dynamikę układu. Całościowy obraz uzyskiwano poprzez uzależnienie „stałych” we wzorze VFT od ciśnienia lub temperatury.
Z czasem pojawiła się koncepcja jednoczesnego uwzględnienia wpływu temperatury i ciśnienia poprzez wykreślenie wszystkich wyników w funkcji tzw. parametru skalowania \(\kappa=\rho^{\gamma}/T\), gdzie \(\rho\) jest gęstością materiału, a \(\gamma\) – stałą materiałową. Okazało się, że przy odpowiednim doborze wartości stałej \(\gamma\) udaje się umieścić wszystkie wyniki np. czasu relaksacji procesu a danej próbki na pojedynczej linii (master curve). Warunkiem przeprowadzenia takiego skalowania jest posiadanie zależności gęstości badanej substancji od temperatury i ciśnienia. Prób takiego skalowania dokonaliśmy w pracach [1] i [2].
- Dreyfus, C; Grand, Le A; Gapiński, J; Steffen, W; Patkowski, A. Scaling the a-relaxation time of supercooled fragile organic liquids Eur Phys J B – Cond Matter and Complex Systems, 42 (3), pp. 309–319, 2004
- Meier, G; Gapinski, J; Ratajczyk, M; Lettinga, M.P.; Hirtz, K; Banachowicz, E; and Patkowski A. Nano-viscosity of supercooled liquid measured by fluorescence correlation spectroscopy: pressure and temperature dependence and the density scaling Submitted to J Chem Phys