Rozpatrujemy proces rozpraszania promieniowania rentgenowskiego lub wiązki neutronów na roztworze/zawiesinie koloidalnej cząsteczek o rozmiarach 1 – 100 nm. Dla uproszczenia zakładamy, że promieniowanie (wiązka neutronów) użyte do pomiarów jest monochromatyczne. Promieniowanie (neutrony) rozproszone wykrywane jest (najczęściej) przez detektory dwuwymiarowe (matryca elementów czułych na promieniowanie jak matryca w aparacie cyfrowym) ustawione w takiej odległości od próbki, że kąt pomiędzy linią łączącą skraj matrycy z próbką a osią optyczną układu nie przekracza kilkunastu stopni (zazwyczaj \(q\) < 5 nm-1).
Z dobrym przybliżeniem natężenie rozproszonego promieniowania można wyrazić jako iloczyn:
\[I(q) = K c M P(q) S(q)\],
gdzie \(K\) jest stałą zależną od właściwości aparatu i próbki, \(c\) jest stężeniem wagowym próbki, \(M\) jest masą molową cząsteczek koloidowych, \(P(q)\) to czynnik kształtu wyrażający wpływ interferencji wewnątrzcząsteczkowych, a \(S(q)\) to czynnik struktury reprezentujący wpływ interferencji międzycząsteczkowych.
Przy znanym stężeniu próbki i stałej masie cząsteczkowej (brak agregacji lub rozpadu) kątowa zależność \(I(q)\) sprowadza się do iloczynu \(P(q)S(q)\).

Relacja pomiędzy natężeniem rozproszonego promieniowania \(I(q)\), czynnikiem kształtu \(P(q)\) i czynnikiem struktury \(S(q)\) obliczonym z modelu Percusa-Yevicka dla twardych kul o ułamku objętościowym \(\phi\) = 10 %.
Z pomiarów SANS lub SAXS otrzymujemy krzywą \(I(q)\). Celem analizy jest wyłuskanie albo \(P(q)\), gdy interesują nas wielkość i kształt cząsteczki koloidowej, albo \(S(q)\), gdy badamy oddziaływania cząsteczek o znanym kształcie. W praktyce te dwie funkcje są ze sobą ściśle powiązane i zmiana jednej z nich automatycznie pociąga za sobą zmianę drugiej.
Bez względu na cel analizy krzywej \(I(q)\), czynnik struktury \(S(q)\) zawsze brany jest z dostępnych modeli teoretycznych, natomiast w ujmowaniu \(P(q)\) spotykane są dwa podejścia:
Podejście pierwsze sprawdza się doskonale przy badaniu oddziaływań cząsteczek o znanym kształcie. Całą analizę można wykonać w domenie \(q\), co automatycznie eliminuje numeryczne błędy transformowania wyników eksperymentalnych do domeny \(r\). Bezpośrednim jej wynikiem jest postać funkcji \(S(q)\), do której dopasowuje się parametry modelu oddziaływań (np. ładunek efektywny). Stosowaliśmy do podejście we wszystkich naszych pracach dotyczących badania struktury i dynamiki koloidów powstałych we współpracy z grupą prof. Jana Dhonta z Forschungszentrum Juelich.
Podejście drugie jest obecnie powszechnie stosowane w analizie wyników SAXS i SANS dla cząsteczek o nieznanym kształcie.
Funkcje \(P(q)\) oraz \(p(r)\) są wzajemnymi transformatami Fouriera,
\[p(r)=\frac{r^2}{2 \pi^2}\int_0 ^\infty P(q) \frac{\sin(qr)}{qr} q^2 \mathrm{d}q\].
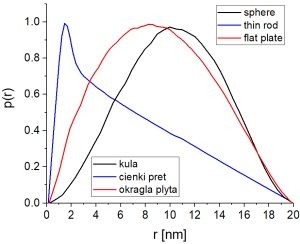
Na powyższym rysunku pokazano (unormowane) funkcje rozkładu odległości par \(p(r)\) dla cząsteczek o trzech różnych kształtach. Krzywe te otrzymano budując modele obiektów z kul rozłożonych na sieci kubicznej (ok. 30 tys. kul na obiekt) i obliczając histogramy odległości między kulami.
Ponieważ numeryczna procedura obliczania transformaty Fouriera z danych dostępnych w ograniczonym zakresie obarczona jest licznymi błędami, w końcu lat 70-tych Otto Glaetter zaproponował metodę pośredniej transformaty Fouriera (Indirect Fourier Transform – IFT) pozwalającą uniknąć tego problemu. Zamiast wykonywać transformatę numeryczną na danych \(I(q)\), zaproponował wyrazić funkcję \(p(r)\) jako kombinację liniową krzywych B-sklejanych \(\varphi_n\) (B-spline),
\[ p(r)=\sum_{n=1}^{M} c_n \varphi_n\],
i ograniczyć oscylacje wysokoczęstotliwościowe poprzez określenie maksymalnego rozmiaru cząsteczki \(D_{max}\). Transformata z \(p(r)\) do \(P(q)\) przybiera wtedy postać:
\[P(q)=4 \pi \int_0 ^{D_{max}} p(r) \frac{\sin(qr)}{qr} \mathrm{d}r = 4 \pi \int_0 ^{D_{max}} \sum_{n=1}^{M} c_n \varphi_n \frac{\sin(qr)}{qr} \mathrm{d}r\],
a ponieważ całki z wyrazów \(\varphi_n \frac{\sin(qr)}{qr}\) są łatwe do obliczenia (\(\varphi_n\) to wielomiany, a zakres \(r\) jest ograniczony do \(D_{max}\)), cała procedura sprowadza się do wyznaczenia współczynników \(c_n\). Algorytm ten przypomina procedurę CONTIN stosowaną powszechnie do wyznaczania rozkładu czasów relaksacji w funkcjach zanikających (np. w dynamicznym rozpraszaniu światła),tym bardziej, że i tu można zastosować wygładzanie (regularization) i więzy nieujemności (nonnegativity).
Cała procedura dopasowania modelu do danych \(I(q)\) wymaga jednoczesnego dopasowania parametrów czynnika struktury \(S(q)\) wziętego z założonego modelu oraz współczynników \(c_n\) funkcji \(p(r)\). W stosunkowo rzadkich przypadkach może się zdarzyć, że oddziaływania będą na tyle słabe by czynnik struktury okazał się stały. Wtedy wystarczy znaleźć same współczynniki \(c_n\).
Warto zauważyć, że z wyznaczonej w ten sposób funkcji \(P(q)\) nie da się łatwo obliczyć rzeczywistego kształtu cząsteczki. Można wyznaczyć pewne parametry charakterystyczne, jak objętość (pierwszy moment \(p(r)\)) i promień żyracji (drugi moment \(p(r)\)). W pewnych charakterystycznych przypadkach można również odgadnąć niektóre cechy kształtu, jak występowanie powłoki, wydłużony kształt, czy wyraźna dwudomenowość.
Kwestia znalezienia kształtu pasującego do \(P(q)\) (lub odpowiadającego mu \(p(r)\)) jest zupełnie niezależnym zagadnieniem. Najciekawsze rozwiązania bazujące na algorytmach genetycznych w zastosowaniu do modlu kulkowego zaproponowała grupa prof. Dmitri Sverguna z EMBL w Hamburgu.